What is “invariant object recognition”?
Humans have the ability to quickly and reliably recognize visual objects, regardless of the viewing angle or distance from which the object is observed. For computers, however, this task was long a challenge. Pattern matching algorithms can be used recognize images. But if an object is viewed from a different angle or distance, it generates a completely different light patterns on the retina or in a camera chip (“pixels”). The ability to robustly recognize objects even when there are variations in viewing angle, distance, or lighting conditions is called “invariant object recognition.”
Temporal correlations as a hint for object identity
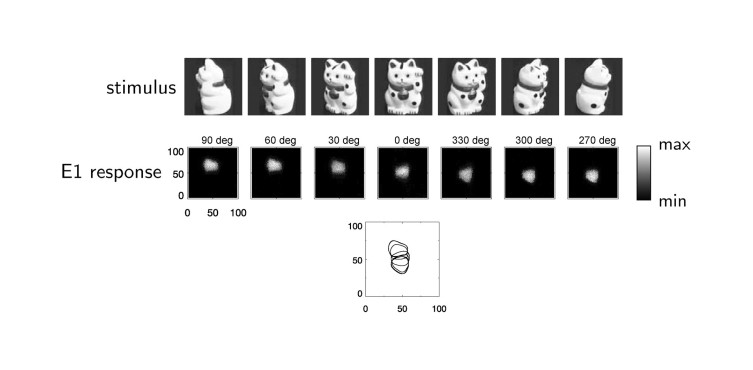
When we move while observing an object, we see different views of this object one after another – in other words, these views are temporally correlated. Utilizing these correlations to learn invariant object representations is the main idea of my paper “Using Spatiotemporal Correlations to Learn Topographic Maps for Invariant Object Recognition” [Michler, Eckhorn, and Wachtler in ‘Journal of Neurophysiology’ (2009)].
In the proposed artificial neural network model, self-organizing neural maps are learned, whose neighborhood relationships are influenced by both similarity (“spatial correlations”) and the temporal sequence (“temporal correlations”) during the learning process.
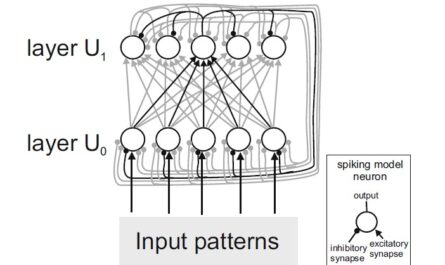
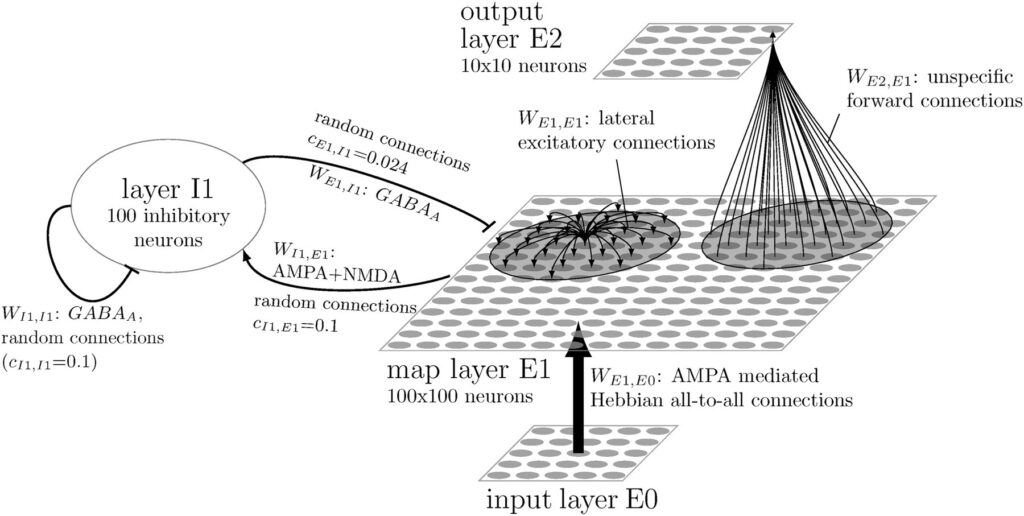
A three layer neural network model
The network model consists of three layers of artificial neurons: E0, E1, and E2. In the input layer E0, the images to be recognized are fed in as pixel patterns, with the brightness of a pixel being used to determine the activity of an input neuron. In the map layer E1, pattern detectors are learned. Lateral inhibition (mediated by a layer of inhibitory neurons I1) prevents all neurons in E1 from being active simultaneously: The most strongly activated neurons activate the inhibitory neurons, which suppress activity of the other neurons in E1. This results in competition among the neurons in E1 and allows different pattern detectors to emerge during learning. The short-range excitatory lateral connections between the E1 neurons cause neighboring neurons to learn similar or consecutively activated input patterns. This results in the formation of neural maps that reflect the temporal and spatial correlations of the learned stimuli.
The results shown in Figures 4 (see above) and 5 of my paper demonstrate that the proposed network model is capable of learning invariant object representations based on temporal correlations.
Biologically plausible spiking neuron models
The individual layers of the network model consist of “spiking” model neurons. Similar to biological neurons, the timing of individual “action potentials” is simulated. Other types of network models, such as “convolutional neural networks” (CNNs) or Transformer models, use model neurons that only consider the average firing rate of individual neurons. With these network models, significant progress has been achieved in recent years: both in object recognition and in other areas such as speech recognition and text completion. These advancements were possible, despite (or perhaps because) the networks are based on substantially simplified model neurons. However, when trying to scale up these models, there are technical limitations regarding available hardware and energy consumption.
Since networks with spiking model neurons generate action potentials (“spikes”) only in a small portion of the neurons at each time step, significantly less information needs to be transmitted to other neurons. When using neuromorphic hardware, substantial efficiency gains might be possible. Therefore, it is still worth to continue exploring network models with “spiking” model neurons (see page 59 in section 4.7 of my doctoral thesis).